Venn Şemaları

Venn şeması nedir?

Venn şeması, birbirlerinin içinden geçen çemberlerden oluşan bir çeşit grafik şemadır. Her çember ayrı bir konsepti veya veri gurubunu temsil eder ve çakışan bölümler paylaştıkları nitelikleri gösterir. Bu da Venn şemasının veri karşılaştırma ve olasılık ölçümü için mükemmel araç olmasını sağlar. Düşüncelerinizi bir Venn şemasına aktardığınızda ilişkilerin ve belirli kalıpların ortaya çıktığını görmeye başlayabilirsiniz ve bu da kararlar almanıza ve karmaşık sistemleri daha iyi anlamanıza yardımcı olabilir. Venn şeması oluşturmak konseptler arasındaki çakışmaları, karşılaştırmaları ve karşıtlıkları görselleştirmeyi kolaylaştırır.

Venn şeması türleri

Venn şeması çeşitli yollarla temsil edilebilir. En çok 3 çemberli Venn şemasına aşinalığınız olabilir, ancak her biri farklı amaçlarla kullanılan birkaç Venn şeması türü vardır.

2 çemberli Venn şeması

Ortada kesişen iki çember.

3 çemberli Venn şeması

Üç çember bir üçlü oluşturur ve ortada kesişir.

4 çemberli Venn şeması

Dört çember bir elmas biçimi oluşturur ve ortada kesişir.

Edwards-Venn şeması

Venn şemasının dördüncü bir versiyonu 1800'lü yıllarda İngiliz biyolog Anthony Edwards tarafından geliştirildi. Ve bunu Edwards-Venn şeması veya EV şeması olarak adlandırdı. EV şeması, 2 ila 4 çember yerine tenis toplarının üzerinde gördüğümüz desenlerden esinlenmiştir. Bu Venn şeması türü çok daha fazla sayıda grubun veya konseptin çakışan özelliklerinin belirlenmesine ve sınıflandırılmasına yardımcı olur. Geleneksel 2, 3 ve 4 çemberli Venn şemaları daha az sayıda veri kümeleri için en uygunken, Edwards-Venn şeması bir konunun daha geniş perspektiflerden analiz edilmesi için uygundur. Ancak, tüm Venn şeması türleri karşılaştırma ve kontrast amacına uygundur.

Venn şeması kullanmanın avantajları

Venn şemasının güzelliği, basitliğinde ve çok yönlülüğünde yatar. Pazarlamadan matematiğe kadar, Venn şeması kullanışlı bir varlıktır. Ekibinizle birlikte yürüttüğünüz çalışmalarda Venn şemaları kullanmanın çeşitli faydalarından bazıları şunlardır.

Beyin fırtınalarında kullanışlıdır

Ekibiniz fikirler bulmak için beyin fırtınası yapmanın ve bir sorunun köküne inmenin hızlı bir yolunu arıyorsa, ihtiyacınız olan şey Venn şeması olabilir. Potansiyel fikirleri temsil etmek için çemberler kullandığınızda, çakışan alanlar nelerin en çok işe yaradığını ve stratejiniz için en uygun olduğunu vurgulamanıza yardımcı olur.

İki öğe arasındaki ilişkileri görün

Bir Venn şemasındaki iki çember çakıştığında, kesişen kısım iki farklı grup arasındaki bağlantı noktasını gösterir. Bu da farklı konular arasındaki ilişkilerin belirlenmesi ve paylaştıkları avantajların daha iyi anlaşılması için son derece kullanışlı olabilir.

Seçenekleri karşılaştırın

Karşılaştırmak ve karşıtlıkları göstermek için kullanılan Venn şeması, işyerinde en çok karşınıza çıkan en popüler grafik araçlarından biridir. Bu eşsiz görsel grafik, ekiplerin çok farklı veri kümeleri arasında somut karşılaştırmalar yapabilmesini sağlayarak bilgiye dayanan kararlar alınmasına olanak tanır.

Bilgiyi görsel olarak düzenleyin ve temsil edin

Görsel grafik, çok farklı insanlardan oluşan bir grubu sezgisel bir anlayışa doğru teşvik etmenin harika bir yoludur. Bir toplantı veya konferans sırasında, bir Venn şeması kullanılması konuşmacıların fikirlerini kolayca anlaşılacak şekilde açıklamalarına ve düzenlemelerine yardımcı olur.

Zor matematik problemlerini çözün

Venn şeması binlerce yıldır matematik ve bilim alanında kullanılıyor. Matematikçi gözüyle bakıldığında, Venn şemaları yalnızca konseptleri veya fikirleri karşılaştırmanın da ötesinde sayıların görsel olarak karşılaştırılmasına ve olasılık sonuçlarına ulaşılmasına yardımcı olabilir.

Venn şeması ne zaman kullanılmalı?

Birçok meslekte ve iş ortamında, öğeler arasındaki ilişkileri ölçmek ve analiz etmek için açıklayıcı bir kaynak olarak Venn şemaları kullanılır. Çok farklı endüstrilerde Venn şemalarının kullanıldığını görebiliriz, örneğin:

Öğretim

Venn şemasının bu kadar farklı endüstride popüler olmasının bir nedeni de, bir çocuğun bile kullanılan simgeleri kolayca yorumlayabileceği kadar basitleştirilebilir olmasıdır. Eğitim Venn şemalarının kullanılması için çok uygundur, çünkü öğrencileri olasılık ve birden fazla nesne arasındaki karşılıklı bağlılık gibi kavramlar ile tanıştırır. Ayrıca, orta öğretimde matematik eğitiminin temelini oluşturur.

Karar alma

Venn şemaları kararlar almanıza yardımcı olabilecek harika bir araçtır. Karar alma sürecinde çakışan bazı faktörleri dikkate almanız gerektiğinde, Venn şeması çizmeniz olası farklı seçenekleri ve sizin için en iyi sonucu verecek olan seçeneği analiz etmenize yardımcı olabilir. Örneğin, bir iş fikirleri listesi hazırlamış ve aralarından hangisinin peşinden gitmek için en iyi fikir olduğuna karar vermeye çalışıyor olabilirsiniz. Venn şeması hangi fikrin aradığınız tüm şartları karşıladığını, yani hem kârlı olduğunu, hem bu fikre talep olduğunu ve hem de sizi heyecanlandıran bir fikir olduğunu göstererek en iyi seçenek üzerinde karar vermenize yardımcı olur.

Matematik

Matematik alanında, Venn şeması sayılar arasındaki mantıksal bağlantıları gösterebilir ve olasılık sonuçlarının belirlenmesini sağlayabilir. Örneğin, bir matematikçi farklı alt küme veya sayı grupları arasındaki korelasyonu göstermek için Venn şeması kullanabilir. Venn şeması veri kümelerini ölçmenize, karşılaştırmanıza ve aralarındaki bağlantıları kurmanıza yardımcı olabileceği için, sayısal değerlerin analizinde bu benzersiz şemanın kullanılması akla uygundur.

İstatistik

Belirli bir olayın sonucunu tahmin etmek veya öngörmek istediğinizde, tüm olasılıkları görselleştirmenize yardımcı olabilecek araçlara ihtiyacınız olur. Bu nedenle, Venn şeması istatistik ve olasılık alanlarında çok kullanışlıdır.

Mantık

Venn şemasının çok doğrudan ve mantıksal bir yapısı var. Farklı konseptleri veya öğeleri eşit konumlandırılmış çemberlere ayırmak, çok farklı fikirlerden oluşan bir grup içindeki ilişkileri görselleştirmeyi ve anlamayı kolaylaştırır.

Bilgisayar bilimi

Modern bilgisayar biliminde Venn şemaları genellikle veri kümeleri arasındaki ilişkileri görselleştirmek için kullanılır. Bunlar farklı sınıfların, kümelerin ve nesnelerin belirli bir bilişim sisteminde birbirleriyle nasıl ilişkili olduğunun anlaşılmasında yardımcı olur ve daha etkili sistemler oluşturmak için farklı kodlama dilleri arasında benzer öğeleri ifade etmek için kullanılabilir.

Dilbilim

Genel dilbilim birbirleriyle bağlantılı yollar ve hiyerarşiler ile doludur. Venn şeması farklı diller ve lehçeler arasındaki karmaşık ilişkiler üzerinde çalışanlar için son derece kullanışlıdır. Bu şema insanların bu bağlantıları kolayca görselleştirmesine olanak tanır.

İş dünyası

Venn şemalarını en yaygın şekilde kurumsal dünyada bulabilirsiniz. İş operasyonları verilerin sürekli olarak karşılaştırılmasını gerektirir. Bu da profesyonellerin gelecek başarı için iş stratejileri belirlemesine ve kampanyalar planlamasına yardımcı olur.

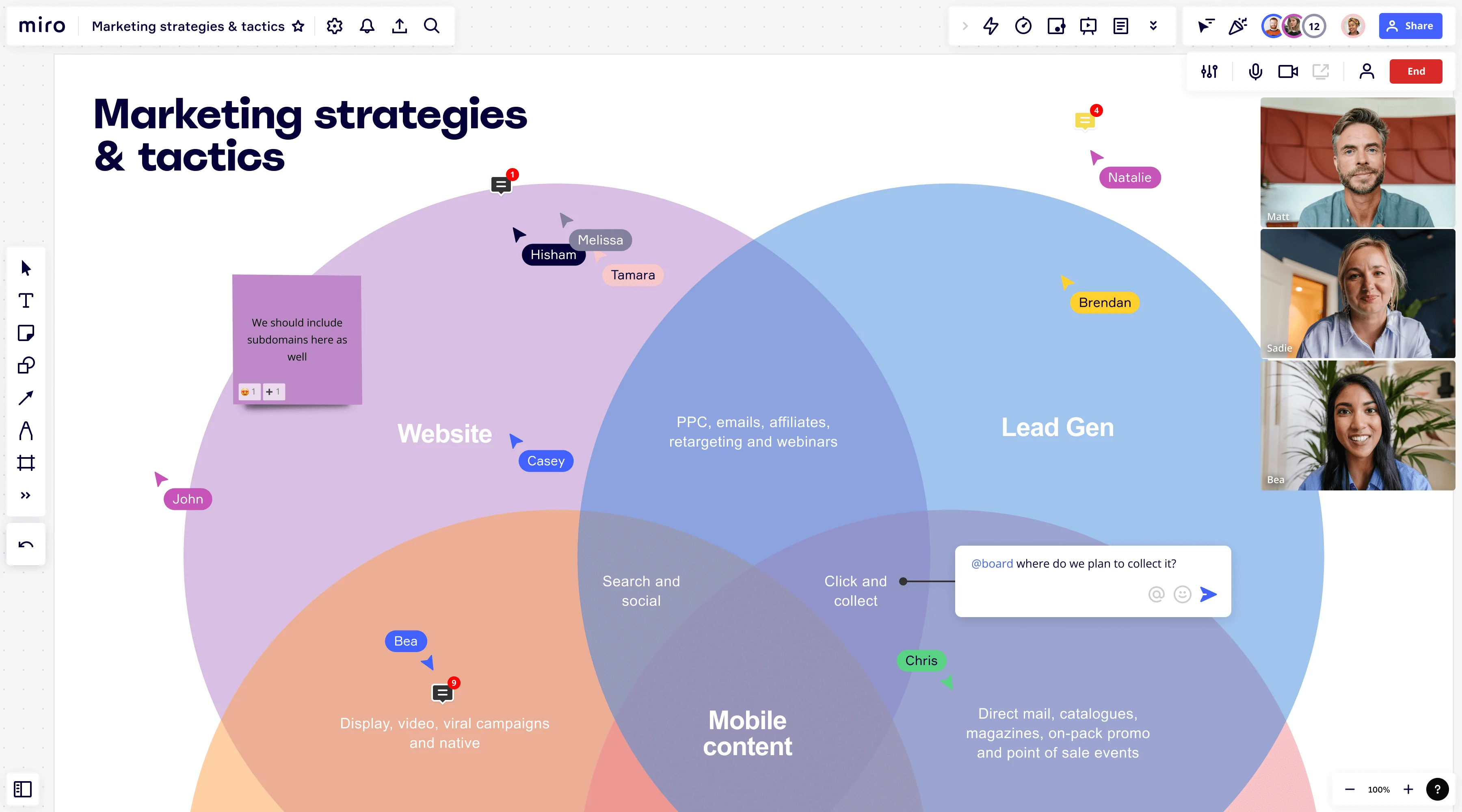
Venn şeması sözlüğü ve sembolleri

Venn şemasının tüm potansiyelini kullanmak istiyorsanız, bu şemayla ilgili bazı sembolleri öğrenmeniz faydalı olacaktır. En önemlileri şunlardır:

Küme

Nesneler veya öğelerden oluşan bir koleksiyon. Her küme kapalı bir şekille, en yaygın olarak bir çember ile gösterilir.

Birleşim (∪)

Tekil fikirleri temsil eden iki şeklin birbirlerine bağlanması. Bu bir birleşim sembolü ∪ ile temsil edilir. Örneğin, A ∪ B ifadesi A kümesinde, B kümesinde veya her ikisinde yer alan tüm öğeleri gösterir.

Kesişim (∩)

Venn şemasının, tüm şekillerin kesiştiği orta noktası. Kesişim ∪ sembolüyle temsil edilir. Bu örnekte, A ∩ B hem A hem de B içinde yer alan tüm öğeleri içerir.

Evrensel küme (U)

Venn şemanızdaki tüm alakalı bilgileri içeren bir küme. Evrensel küme U olarak veya bazen ξ işaretiyle gösterilir.

Boş küme (Ø)

Hiçbir öğe içermeyen bir küme.

Tümleyen (')

Evrensel küme içindeki öğelerden oluşan bir küme. Bir A kümesinin tümleyeni (A' veya bazen Ac olarak gösterilir) evrensel küme içinde olan, ancak A içinde yer almayan tüm öğeleri içerir.

Venn şeması nasıl oluşturulur

Venn şeması oluşturmanın çok farklı yolları vardır. Ancak doğru şablonun kullanılması, karşılaştırma ve karşıtlıkları gösterme analizlerinin biçimlendirilmesine ve yapılandırılmasına yardımcı olabilir. Miro'nun sezgisel Venn Şeması Şablonunukullanarak nasıl Venn şeması çizebileceğinizi burada görebilirsiniz:

Adım 1

İlk olarak tarif etmek istediğiniz tüm nesneleri, öğeleri ve fikirleri yazın. Bu veri koleksiyonu sizin evrensel kümeniz olacak.

Adım 2

Daha sonra, en uygun Venn şeması türünün hangisi olacağına karar verin. Örneğin, üç küme arasındaki benzerlikleri ve farklılıkları bulmak için 3 çemberli Venn şeması kullanmalısınız.

Adım 3

Her veri kümesi için bir çember çizin. Şablonda halihazırda her küme için üç çember bulunur ve gerektiği şekilde çember ekleyebilir veya silebilirsiniz.

Adım 4

Diğer kümelerle benzerliklerine veya farklılıklarına dayanarak her bir öğeyi şemanıza ekleyin. Diğer kümelerle benzerlikleri olmayan öğeler her bir kümeye karşılık gelen çemberlere gider: A, B veya C. Eğer bir öğe A ve B ile benzerlik taşıyorsa, bu iki çemberin çakıştığı bölüme gider. Bu sizin Venn şemanızın birleşimine dahil edilir.

Bir öğenin belirleyici niteliği A, B ve C ile paylaşılıyorsa, bu öğe şemanın merkezinde tüm çemberlerin kesiştiği bölüme gider. Bu da şemanızın kesişimi olur.

Adım 5

Tüm kümeler şemanıza eklendikten sonra, Venn şemanızı renkler, etiketler ve notlarla kişiselleştirmenizin zamanı gelmiştir. Venn şemanızı ekibinizle paylaşın ve ekip üyelerinizi etiketleyerek onlardan kendi girişlerini yapmalarını ve geri bildirim vermelerini isteyin.

Venn şemaları ve kümeler teorisi

Venn şemalarının çeşitli alanlarda ne kadar kullanışlı olduğunu daha önce tartıştık. Şimdi de Venn şemalarının matematiğin kümeler teorisi adı verilen dalında nasıl kullanıldığına bakalım. Kümeler teorisi, bir nesnenin paylaşılan ve tekil özelliklerine eğilen matematik dalıdır. ‎2, 3 ve 4 çemberli Venn şeması matematiğin bu alanında kullanılır. Kümeler teorisinin temelinde yatan süreç Venn şemasının yapısıyla çok uyumludur, çünkü her ikisi de aynı anda çok sayıda nesnenin (veya sayının) karşılaştırılmasıyla ilgilidir. Örneğin, Venn şeması bir grup sayının hangi özellikleri paylaştığını belirlemek için bir kümeler teorisi denkleminin temsil edilmesine yardımcı olabilir. "Küme" bir nesneler koleksiyonudur ve her nesne toplamın içindeki tek bir öğeyi temsil eder. 2 çemberli Venn şemamız olduğunu düşünelim. Bir çember kırmızı, diğer mavi olsun. Bunlar bizim iki nesnemiz. Bu nesnelerin çakıştığı orta noktaya kesişim adı verilir. Bu kesişimin içinde kalan alan şimdi kırmızı ve mavinin paylaştığı niteliği temsil eder: yani mor. Bu süreç tüm nesnelere ve onların birbirleriyle çakışan benzerliklerine uygulanabilir. Renklerden sayılara ve sporlara kadar her nesne küme teorisi ve Venn şeması perspektifinden karşılaştırılabilir.

Venn şemasıyla olasılık hesaplama

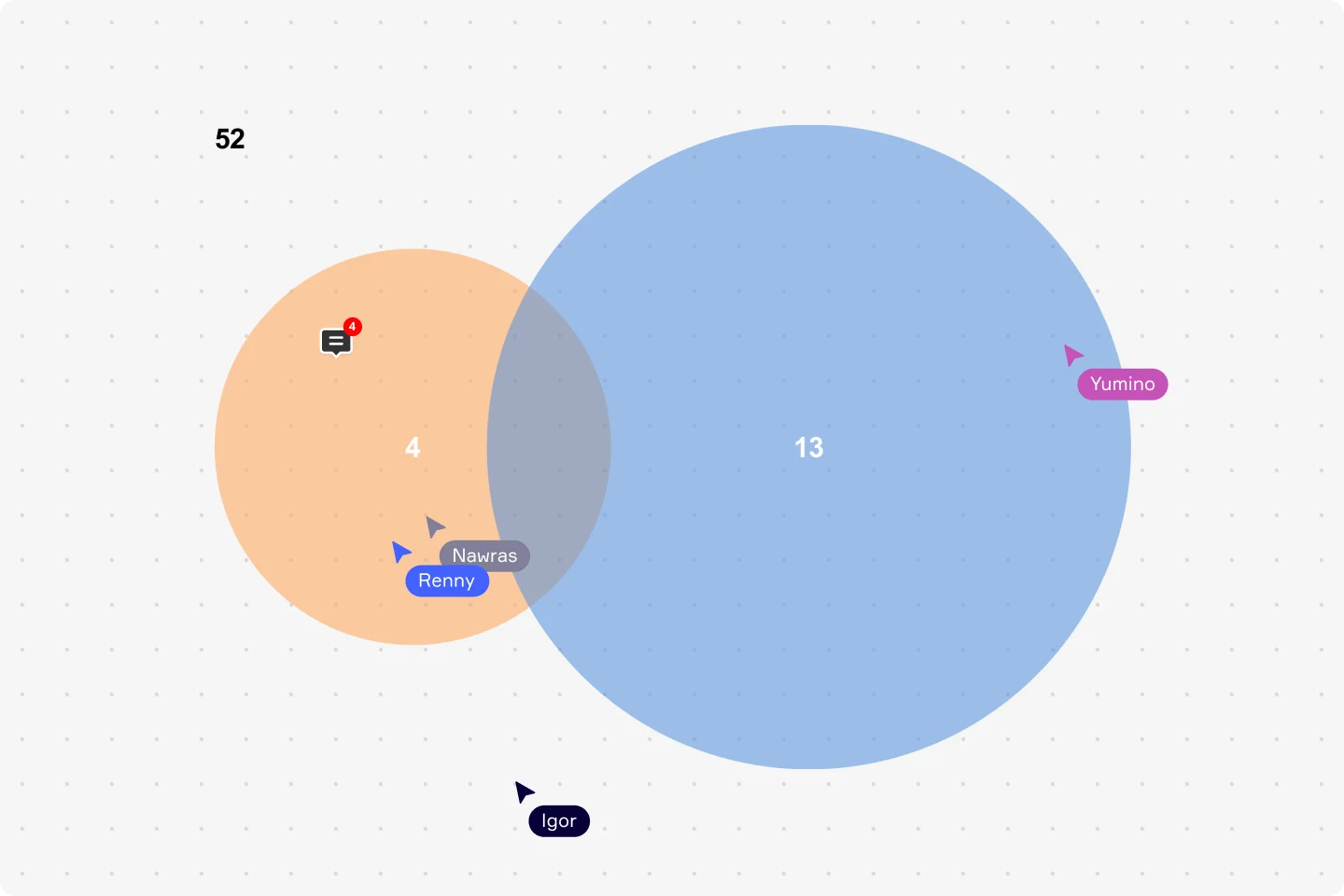
Venn şemalarının yaygın olarak kullanıldığı diğer bir alan olasılık hesaplarıdır. Venn şeması olasılığı, bir senaryonun sonucunu tahmin etmek için kullanılan matematiğin bir ürünüdür. Örneğin, bir olayın meydana gelme olasılığını hesaplamak için 2 çemberli Venn şeması kullanabilirsiniz. Bunun için çemberlerin içine konseptler veya fikirler yerine sayılar yazılır. Venn şemalarının farklı olayların olasılıklarını hesaplamak amacıyla nasıl kullanıldığını göstermek için bir iskambil destesini kullanalım. Bir iskambil destesinde jokerler hariç 52 kart bulunur. Deste dört simgeden oluşur ve her simgede 13 farklı kart bulunur. Diyelim ki desteden Kız veya Kupa çekme olasılığını bilmek istiyoruz. Dikdörtgen tüm sonuçları temsil eder, yani 52 kartın tümünü. Bir destede dört kız olduğundan, kız çekme olasılığı 4/52 olur. Kupa çekme olasılığıysa 13/52 olur. Ancak bu kartlardan biri her iki kategoriye de girer: hem Kız, hem de Kupa (yani Kupa Kızı). Çemberler, bu kartın her iki kümeye de girdiğini göstermek için çakışır. Sonuçların bir Venn şemasıyla görselleştirilmesi Kupa Kızını iki kez saymaktan kaçınmanızı sağlar. Venn şemasına dayanarak şu hesaplamayı yapabilirsiniz: 4+13-1 = 16. Kız veya Kupa çekme olasılığı 16/52 olur. Bunun gibi bir hesaplama, örneğin bir projenin başarısı, kaç müşteri beklenebileceği veya bir pazarlama kampanyasının sonucu gibi çok çeşitli olayların veya durumların olasılığını belirlemekte insanlara yardımcı olabilir. Olasılık işletmelerin başarıyı takip etme yollarının büyük bir parçasını oluşturur.

Karşılaştırmak ve karşıtlıkları göstermek için Venn şemalarını kullanma

Venn şemasının en popüler kullanımlarından biri, fikirleri birbirleriyle karşılaştırarak ve karşıtlıklarını göstererek beyin fırtınası yapma aracı olarak kullanımıdır. Karşılaştırmak ve karşıtlıkları göstermek için kullanılan Venn şemasını görsel olarak kavramak kolaydır ve kolay yorumlama için basit yapılara ayrılabilir. Örneğin, bir karşılaştırma ve karşıtlıkları gösterme denemesi yazıyorsanız, seçtiğiniz konular arasındaki temel farklılıkları aydınlatmak için Venn şeması kullanabilirsiniz. İkna edici bir karşılaştırma ve karşıtlıkları gösterme denemesi yazmak için, konularınızın temel özelliklerini ve farklılıklarını derinlemesine anlamanız gerekir. Karşılaştıracağınız temel konuları temsil etmesi için birbirleriyle kesişen 2 ila 4 çember çizerek başlayın. Daha sonra, çakışan alanları kesişen konuların paylaştığı özelliklerle doldurun. Dışarıdaki, bağlantılı olmayan alanlar, ilgili konunun benzersiz özellikleriyle doldurulabilir ve böylece farklılıkları temsil eder. Ortadaki kesişim tüm konularınızı birbirine bağlayan özellikleri temsil eder. Bir karşılaştırma ve karşıtlıkları gösterme denemesi yazmadan önce, konularınızın birbirleriyle nasıl ilişkili olduklarını ve ne açıdan farklı olduklarını daha net bir şekilde görmek için bir Venn şeması kullanmayı düşünebilirsiniz.

Venn şemaları ve Euler şemaları

Venn şemasına çok benzeyen diğer bir şema da Euler şemasıdır. Hem Euler hem de Venn şemaları kümeler teorisine dayanır ve kümeler arasındaki ilişkileri gösteren çemberlerden oluşur. Ancak, bunlar aynı şey değildir. Venn şeması farklı kümeler arasındaki tüm olası ilişkileri gösterir. Buna varsayımsal olarak olası ilişkiler de dahildir. Venn şemaları, öğeler arasındaki kesişimlerin tüm olası kombinasyonlarını içerir. Euler şeması yalnızca zaten mevcut olan kesişim kombinasyonlarını veya ilişkileri gösterir. Birbirini içeren, birbirlerinden ayrı olan veya kesişen çemberler içerir. Bir şemanın, Venn şeması mı yoksa Euler şeması mı olduğunu belirlemek için önemli bir ipucu boş kesişim olup olmadığına bakmaktır. Venn şemalarında, boş olsalar bile kümeler arasındaki tüm kesişimler gösterilmelidir. Ancak Euler şeması yalnızca boş olmayan kesişimleri gösterir. Euler şemaları genellikle Venn şemalarına kıyasla daha karmaşıktır. Karmaşık hiyerarşileri açıklamak, çakışan tanımları göstermek ve bir mantıksal argümanın geçerli olup olmadığı belirlemek için kullanılır.

Venn şeması örneği

İş dünyasında Venn şemasının nasıl kullanıldığıyla ilgili bir örneği burada görebilirsiniz. Daha standartlaştırılmış bir iş akışı için bir organizasyondaki farklı ekiplerin rollerini ve sorumluluklarını karşılaştırmanızın gerektiği durumu ele alalım. Pazarlama ekipleri ve web geliştirme ekipleri arasındaki ilişkiyi tarif etmek istiyorsunuz. Pazarlama ekipleri veri analitiğini, hukuki meseleleri, tüketici araştırmalarını, sosyal medya temsilini ve marka yönetimini ele alır. Web geliştirme ekipleri UX ve UI tasarımını, marka yönetimini, kalite testlerini, SEO analizini, proje yönetimini, tüketici araştırmalarını ve veri analitiğini ele alır. Bu Venn şeması örneğinde, kesişim tüm çakışan sorumluluk alanlarını içerir: veri analitiği, marka yönetimi ve tüketici araştırması. Bunlar pazarlama ve web geliştirme ekiplerinin işbirliği yapabileceği alanlardır. Venn şeması örnekleri her tür nesne veya öğe arasındaki ilişkileri ve farklılıkları tasvir edebilir. Venn şemaları işyerinde kullanıldığında, beyin fırtınası, strateji geliştirme ve argümanları karşılaştırma veya karşıtlıklarını gösterme gibi alanlarda sorunların özüne inen bilgilere ulaşılmasını sağlar.