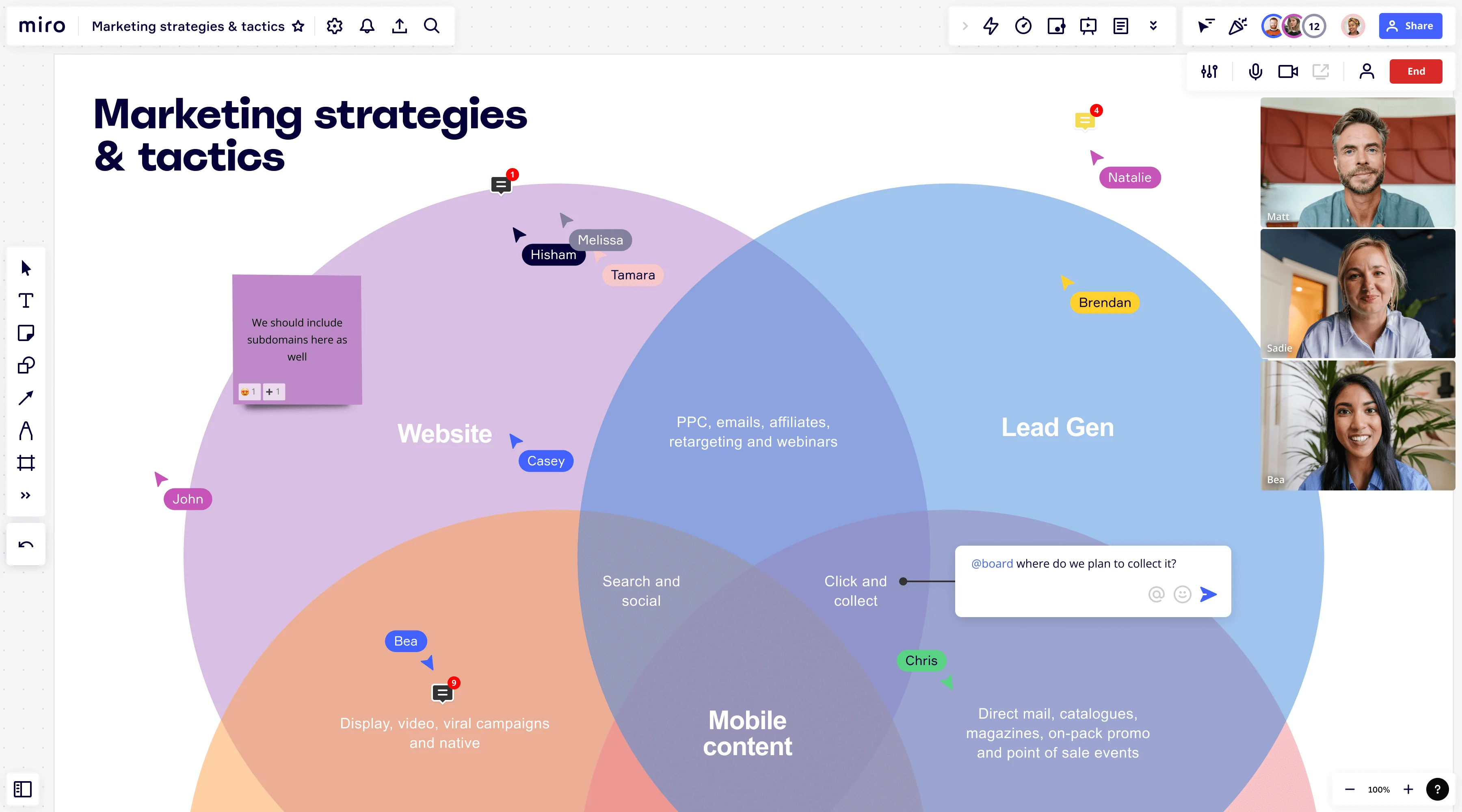
Venn-diagrammer

Hva er et Venn-diagram?

Et Venn-diagram er et diagram som består av overlappende sirkler. Hver sirkel representerer et konsept eller en datagruppe, med overlappende deler som representerer deres felles egenskaper. Dette gjør Venn-diagrammer til et utmerket verktøy for datasammenligning og måling av sannsynlighet. Ved å uttrykke tankene dine i form av et Venn-diagram kan du begynne å se relasjoner og mønstre, noe som deretter kan hjelpe deg med å ta beslutninger eller bedre forstå komplekse ting. Å opprette et Venn-diagram gjør det enkelt å visualisere hvordan ulike konsepter overlapper hverandre, hva de har felles, og hva som skiller dem.

Forskjellige Venn-diagrammer

Et Venn-diagram kan fremstå på flere forskjellige måter. Du er kanskje mest kjent med Venn-diagrammer som har tre sirkler, men det finnes flere typer Venn-diagrammer, som brukes til forskjellige ting.

Venn-diagram med to sirkler

To sirkler som overlapper hverandre i midten.

Venn-diagram med tre sirkler

Tre sirkler i en trekantform med overlapping i midten.

Venn-diagram med fire sirkler

Fire sirkler i en diamantform med overlapping i midten.

Edwards-Venn-diagram

En fjerde versjon av Venn-diagrammet ble utviklet på midten av 1800-tallet av en britisk biolog som het Anthony Edwards. Han kalte det Edwards-Venn-diagrammet, eller EV-diagrammet. I stedet for å ha 2–4 sirkler er EV-diagrammet inspirert av formen til en tennisball. Denne typen Venn-diagram bidrar tli å identifisere og klassifisere overlappende egenskaper mellom et mye større antall grupper eller konsepter. Mens de tradisjonelle Venn-diagrammene med 2, 3 og 4 sirkler er best egnet til mindre grupper av datasett, er Edwards-Venn-diagrammet best egnet til å analysere et emne fra et bredere utvalg perspektiver. Imidlertid tjener alle typer Venn-diagrammer formålet med sammenligning og kontrast.

Fordelene ved et Venn-diagram

Det flotte med Venn-diagrammer er ikke enkeltheten, men fleksibiliteten. Venn-diagrammet er nyttig i veldig mange sammenhenger, i alt fra markedsføring til matematikk. Her er noen av de mange fordelene ved å bruke Venn-diagrammer i teamet ditt.

Nyttig ved idémyldring

Hvis teamet ditt er ute etter en rask måte å idémyldre på og komme til roten av et problem, kan et Venn-diagram være akkurat det du trenger. Ved å bruke sirklene til å representere potensielle ideer kan de overlappende områdene bidra til å fremheve hva som fungerer best og er mest gunstig for strategien din.

Se forholdet mellom to elementer

Når to sirkler i et Venn-diagram overlapper hverandre, viser den overlappende delen forbindelsespunktet mellom de to forskjellige gruppene. Dette kan være ekstremt nyttig for å identifisere forholdene mellom forskjellige emner, og få en dypere forståelse av delte fordeler.

Sammenlign valg

Et Venn-diagram som brukes til sammenligning og kontrast, er et av de mest populære du vil finne på arbeidsplassen. Dette unike visuelle diagrammet lar teamet se håndgripelige sammenligninger mellom svært forskjellige datasett, noe som gir mulighet for mer informert beslutningstaking.

Visualisere, organisere og presentere informasjon

Et visuelt diagram kan hjelpe andre til å forstå ting på en enkel måte. Under et møte eller en konferanse kan bruken av et Venn-diagram hjelpe talere med å kommunisere og organisere ideene sine på en lettforståelig måte.

Løse vanskelige matteproblemer

Venn-diagrammet har blitt brukt i tusenvis av år innen matematikk og vitenskap. Når Venn-diagrammer brukes i matematikken, kan de visuelt sammenligne tall og komme med sannsynlighetskonklusjoner, i stedet for å bare sammenligne konsepter eller ideer.

Når du skal bruke et Venn-diagram

Mange yrker og miljøer bruker Venn-diagrammet som en kilde som måler og dissekerer forhold mellom elementer. Du kan finne Venn-diagrammer i en rekke forskjellige bransjer, blant annet:

Undervisning

En del av det som gjør Venn-diagrammet så populært i så mange forskjellige bransjer, er det forhold at det kan forenkles til et punkt der selv et barn enkelt kan tolke symbolene. Utdanning er et flott sted å bruke Venn-diagrammet, fordi det introduserer studenter for konsepter som sannsynlighet og sammenheng mellom flere objekter. Det hjelper også med å legge grunnlaget for å lære matematikk på videregående skole.

Beslutningstaking

Venn-diagrammer er et flott verktøy som hjelper deg med å ta beslutninger. Når du må vurdere flere faktorer som overlapper for å ta en beslutning, kan det å lage et Venn-diagram hjelpe deg med å analysere de forskjellige alternativene som er tilgjengelige, og hvilket som vil gi deg det beste resultatet. For eksempel kan du lage en liste over forretningsideer, og prøve å bestemme hvilken idé som er best å arbeide videre med. Et Venn-diagram kan hjelpe deg med å bestemme det beste alternativet, ved å identifisere hvilket som treffer best når det gjelder lønnsomhet, etterspørsel og andre ting som er viktige for deg.

Matematikk

Innen matematikk kan et Venn-diagram illustrere logiske forbindelser mellom tall og bestemme sannsynlighetsresultater. For eksempel kan en matematiker bruke et Venn-diagram til å vise sammenhengen mellom forskjellige grupper av delmengder eller tall. Og siden et Venn-diagram kan hjelpe deg med å måle, sammenligne og koble sammen datasett, gir det mening at dette unike diagrammet kan brukes til å analysere numeriske verdier.

Statistikk

Når du skal estimere eller forutsi utfallet av en bestemt hendelse, trenger du et verktøy som hjelper deg med å visualisere alle potensialene. Av denne grunn har Venn-diagrammet vært viktig innenfor statistikk og sannsynlighet.

Logikk

Det er noe veldig enkelt og logisk med strukturen til et Venn-diagram. Å skille forskjellige konsepter eller elementer i like posisjonerte sirkler gjør det lettere å visualisere og forstå forholdene mellom flere ideer.

Datavitenskap

I moderne datavitenskap brukes Venn-diagrammer ofte for å visualisere relasjoner mellom datasett. De er nyttige for å forstå hvordan forskjellige klasser, sett og objekter forholder seg til hverandre innenfor et gitt datasystem, og de kan brukes til å uttrykke lignende elementer mellom forskjellige kodespråk for å skape mer effektive systemer.

Lingvistikk

Global lingvistikk er full av sammenkoblede veier og hierarkier. Venn-diagrammet er ekstremt nyttig for dem som studerer de komplekse forholdene mellom forskjellige språk og dialekter. Dette diagrammet lar folk visualisere disse forbindelsene på en enkel måte.

Næringsliv

Du finner ofte Venn-diagrammer i næringslivet. Forretningsdrift krever konstant sammenligning av data. Dette hjelper fagfolk med å sette opp forretningsstrategier og kampanjer for fremtidig suksess.

Venn-diagrammet: ordliste og symboler

Det er mange symboler i et Venn-diagram som kan være nyttige å kjenne til hvis du vil få mest mulig ut av diagrammet. De viktigste er:

Sett

En samling objekter eller elementer. Hvert sett er representert ved en lukket form, vanligvis en sirkel.

Union (∪)

To figurer (som representerer individuelle ideer) henger sammen. Dette er representert med unionssymbolet (∪). For eksempel angir A ∪ B alle elementer som er i sett A eller B, eller i begge.

Snitt (∩)

Midtpunktet i et Venn-diagram, hvor alle formene krysser hverandre. Snittet er representert med symbolet ∩. I dette eksemplet inkluderer A ∩ B alle elementene som er i både A og B.

Universal mengde (U)

Et sett som inneholder all relevant informasjon fra Venn-diagrammet. Universalmengden betegnes som U eller noen ganger ξ.

Tom mengde (Ø)

Et sett som ikke har noen elementer.

Komplement (')

Et sett som består av elementene som finnes i den universale mengden. Komplementet til et sett A (betegnet med A' eller noen ganger Ac) og inkluderer alle elementer som ikke er i A, men som er i den universale mengden.

Hvordan opprette et Venn-diagram

Det er mange forskjellige måter å lage et Venn-diagram på. Men ved å bruke rett mal kan du få hjelp til å formatere og strukturere enhver sammenlignings- eller kontrastanalyse. Slik lager du et Venn-diagram ved hjelp av Miros intuitive mal. Mal til Venn-diagram:

Trinn 1

Skriv først ned alle objektene, elementene og ideene du vil skildre. Denne datasamlingen er den universale mengden.

Trinn 2

Deretter bestemmer du hvilken type Venn-diagram som er best egnet. For å finne likhetene og forskjellene mellom tre sett bør du for eksempel bruke et Venn-diagram med tre sirkler.

Trinn 3

Tegn én sirkel for hvert datasett. Malen har allerede tre sirkler for hvert sett, og du kan legge til og slette sirkler etter behov.

Trinn 4

Legg til hvert element i diagrammet ditt avhengig av om de har likheter eller forskjeller med de andre settene. Elementer uten likheter vil gå i en av sirklene for hvert sett: A, B eller C. Hvis det er en likhet mellom et element fra A og B, vil dette elementet gå inn i den overlappende delen av disse to sirklene. Dette vil bli inkludert i unionen i Venn-diagrammet ditt.

Hvis karakteristikken til et element deles med A, B og C, vil dette elementet gå inn i midten av diagrammet, der alle sirklene krysser hverandre. Dette vil være snittet i diagrammet.

Trinn 5

Når alle settene dine er lagt til diagrammet, er det på tide å tilpasse Venn-diagrammet med farger, etiketter og notater. Del Venn-diagrammet med teamet ditt, og be medlemmene dine om innspill og tilbakemeldinger.

Venn-diagrammer og sett-teorien

Vi har tidligere diskutert hvordan Venn-diagrammer er nyttige på flere områder. La oss se på hvordan Venn-diagrammer brukes i en gren av matematikken som kalles sett-teori. Sett-teori er en gren av matematikken som omhandler et objekts delte og individuelle egenskaper. Venn-diagrammet med to, tre og fire sirkler brukes i dette segmentet av matematikken. Prosessen bak sett-teorien harmonerer godt med strukturen til et Venn-diagram. fordi de begge tar for seg å sammenligne flere objekter (eller tall) samtidig. For eksempel kan et Venn-diagram bidra til å illustrere en sett-teori-ligning for å bestemme hvilke egenskaper som er delt av en gruppe tall. Et «sett» er en samling av objekter der hvert objekt representerer et enkelt element av helheten. La oss si at vi har et Venn-diagram med to sirkler. Én sirkel er rød, og den andre er blå. Dette er de to objektene. Midtpunktet der disse to objektene overlapper hverandre, kalles snittet. Plassen innenfor snittet representerer nå kvaliteten som rødt og blått deler: lilla. Denne prosessen kan brukes på alle objekter og deres relative overlappende likheter, fra farger til tall til sport. Alle objekter kan sammenlignes gjennom med sett-teori og et Venn-diagram.

Beregning av sannsynlighet med et Venn-diagram

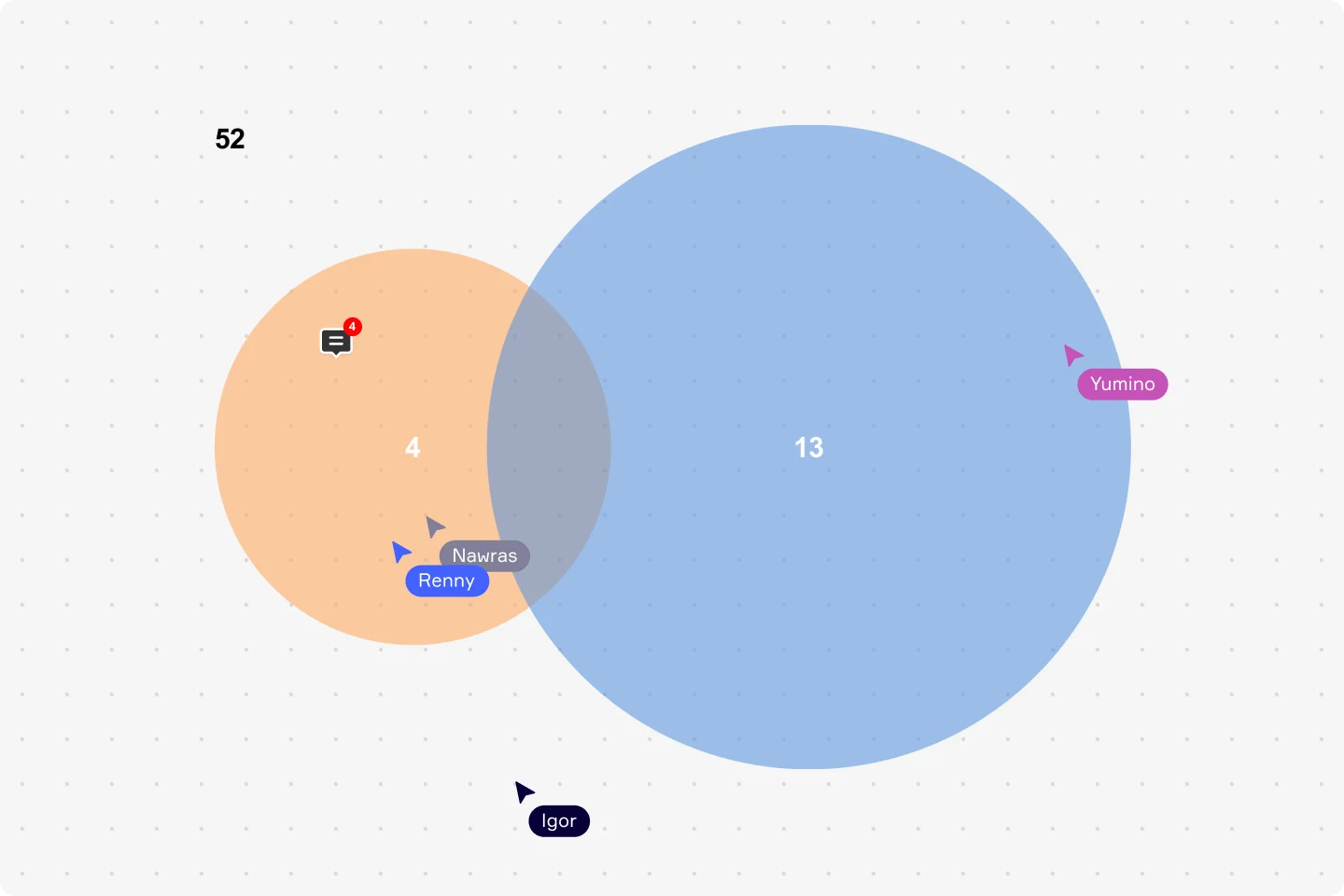
Et annet område hvor Venn-diagrammer brukes mye, er når du skal beregne sannsynlighet. Venn-diagrammets sannsynlighet er et produkt av matematikk som brukes til å forutsi utfallet av et scenario. Du kan for eksempel bruke et Venn-diagram med to sirkler til å beregne sannsynligheten for at en hendelse skal inntreffe. De ville gjøre dette ved å sette inn tall i stedet for konsepter eller ideer i sirklene. La oss bruke eksemplet med en pakke med spillekort for å vise hvordan Venn-diagrammer brukes til å beregne sannsynligheten for forskjellige hendelser. En kortstokk består av 52 kort i tillegg til jokere. Pakken består av fire farger med 13 kort i hver farge. Du vil vite sannsynligheten for å trekke en dronning eller en hjerter. Rektangelet representerer alle utfallene, som er alle de 52 kortene. Siden det er fire dronninger i en pakke, er muligheten for å velge en dronning 4/52. Sannsynligheten for å velge en hjerter, er 13/52. Men ett av disse kortene er begge – en dronning og en hjerter (hjerter dronning). Sirklene overlapper hverandre for å vise at dette kortet er i begge settene. Ved å visualisere resultatene med et Venn-diagram, sikrer du at du ikke teller hjerterdronningen to ganger. Basert på Venn-diagrammet vil du bruke følgende beregning: 4+13-1 = 16. Sannsynligheten for å velge en dronning eller en hjerter er 16/52. En beregning som dette kan hjelpe folk med å bestemme sannsynligheten for en lang rekke hendelser eller situasjoner, for eksempel suksessen til et prosjekt, hvor mange kunder de kan forvente, eller resultatet av en markedsføringskampanje. Sannsynlighet utgjør en stor del av hvordan bedrifter sporer og måler suksess.

Bruke Venn-diagrammer til sammenligninger og kontraster

En av de mest populære bruksområdene for Venn-diagrammet er som et verktøy for idémyldring ved å sammenligne dem og sette dem opp mot hverandre. Et Venn-diagram for sammenligning og kontrast er lett å forstå visuelt og kan brytes ned i enkle strukturer for enkel tolkning. Hvis du for eksempel skal skrive et essay med sammenligning og kontrast, kan du bruke et Venn-diagram til å belyse hovedforskjellene mellom de valgte emnene. For å skrive et overbevisende essay med sammenligning og kontrast trenger du en dyp forståelse av emnenes medfødte egenskaper og forskjeller. Start med å tegne 2-4 overlappende sirkler som representerer hovedemnene eller sammenligningsemnene dine. Deretter fyller du opp de overlappende områdene med egenskaper som de kryssende emnene deler. De ytre, ikke-sammenhengende rommene kan fylles med egenskaper som er unike for emnet og dermed representere forskjellene. Det sentrale skjæringspunktet (snittet) vil representere det som binder alle emnene dine sammen. Før du skriver et sammenlignings- og kontrastessay, kan du vurdere å bruke et Venn-diagram for å gi et klarere bilde av hvordan emnene dine er relatert til hverandre – og hvordan de ikke er det.

Venn-diagram vs Euler-diagram

En annen type diagram som ligner veldig på et Venn-diagram, er Euler-diagrammet. Både Euler- og Venn-diagrammer er basert på sett-teori og består av sirkler som viser sammenhengene mellom settene. De er imidlertid ikke helt like. Et Venn-diagram viser alle mulige sammenhenger mellom ulike sett. Dette inkluderer forhold som er hypotetisk mulige. Venn-diagrammer inkluderer alle mulige kombinasjoner av skjæringspunkter (snitt) mellom elementene. Et Euler-diagram viser bare snittkombinasjonene eller relasjonene som allerede eksisterer. Den inkluderer sirkler som enten inkluderer, ekskluderer eller krysser hverandre. Et nøkkeltips for å identifisere om et diagram er et Venn- eller Euler-diagram, er å se om det er et tomt snitt. Med Venn-diagrammer må du avbilde hvert snitt mellom settene, selv om snittet er tomt. Men et Euler-diagram viser bare snitt som ikke er tomme. Euler-diagrammer har en tendens til å være mer kompliserte enn Venn-diagrammer. De brukes til å forklare komplekse hierarkier, skildre overlappende definisjoner og avgjøre om et logisk argument er gyldig.

Eksempel på Venn-diagram

Her er et praktisk eksempel på hvordan du bruker et Venn-diagram i forretningsverdenen. La oss si at du må sammenligne rollene eller ansvaret til forskjellige team i en organisasjon for en mer strømlinjeformet arbeidsprosess. Du ønsker å skildre forholdet mellom markedsføringsteam og nettutviklingsteam. Markedsføringsteam håndterer dataanalyse, juridisk administrasjon, forbrukerundersøkelser, representasjon i sosiale medier og varemerkestyring. Webutviklingsteam håndterer UX- og UI-design, varemerkestyring, kvalitetstesting, SEO-analyse, prosjektledelse, forbrukerundersøkelser og dataanalyse. I dette Venn-diagrameksemplet vil snittet inkludere alle de overlappende ansvarsområdene: dataanalyse, varemerkestyring og forbrukerundersøkelser. Dette vil være områder der markedsførings- og nettutviklingsteam kan samarbeide. Venn-diagram-eksempler kan illustrere relasjonene og forskjellene mellom objekter eller elementer. På arbeidsplassen gir et Venn-diagram dyptgående innsikt for idémyldring, strategiutvikling og sammenligning eller kontrasterende argumenter.