مخططات فين

ما هو مخطط فين؟
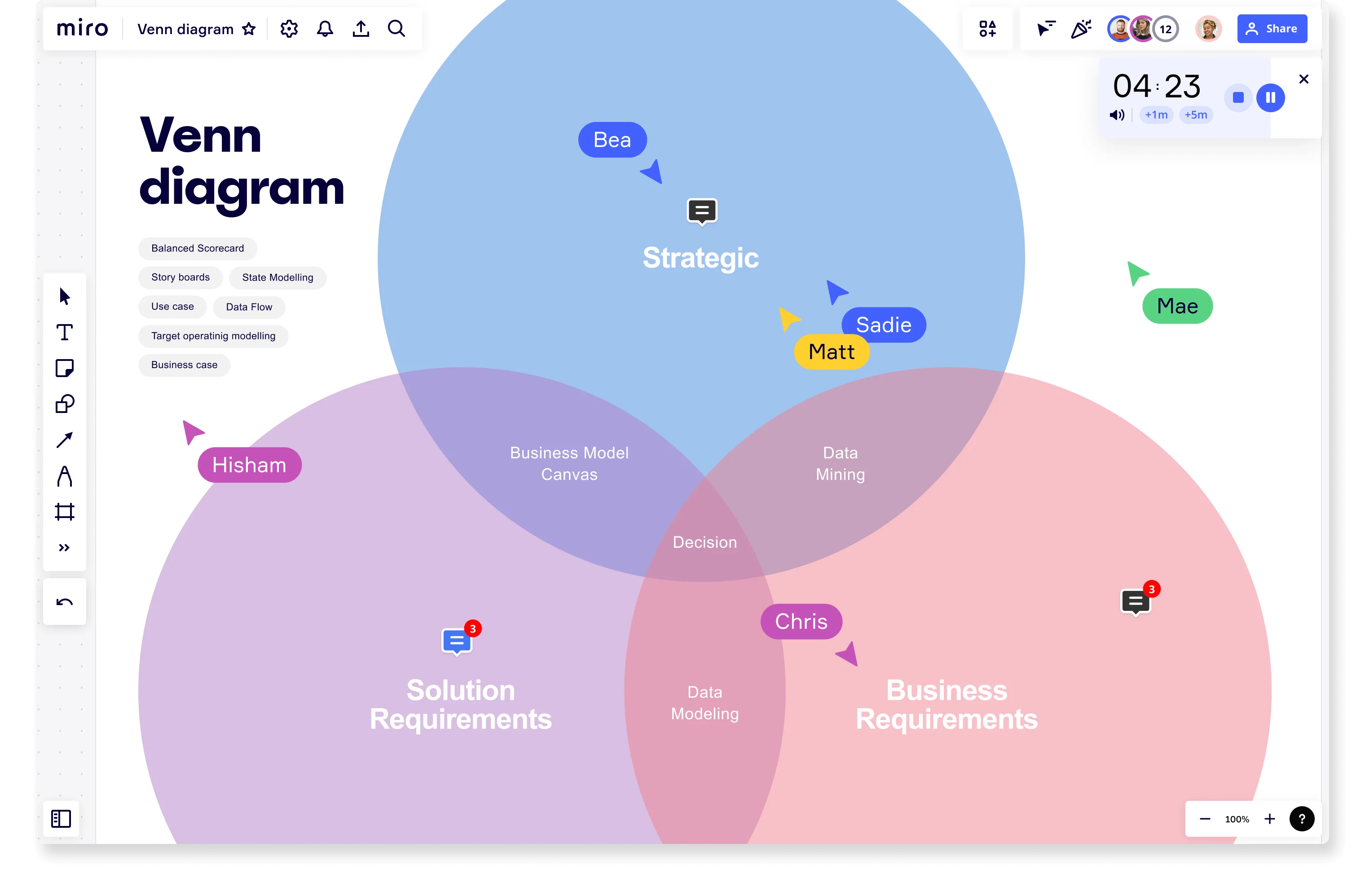
مخطط فين هو نوع من المخططات الرسومية المشكل من دوائر متداخلة. تمثل كل دائرة مفهومًا أو مجموعة بيانات مختلفة، مصحوبة بأقسام متداخلة تمثل الصفات المشتركة. وهذا يجعل مخططات فين أداة ممتازة لمقارنة البيانات وقياس الاحتمالية. من خلال رسم أفكارك على مخطط فين، يمكنك البدء في رؤية العلاقات والأنماط تظهر، والتي يمكن أن تساعدك بعد ذلك على اتخاذ القرارات أو فهم المفاهيم المعقدة بشكل أفضل. إنشاء مخطط فين يجعل من السهل تصور كيفية تداخل المفاهيم والمقارنة والتباين.
أنواع مخططات فين
يمكن تمثيل مخطط فين بعدة طرق. قد تكون اعتدت أكثر على مخطط فين المكون من 3 دوائر، ولكن هناك عدة أنواع من مخططات فين ويُستخدم كل منها لسبب مختلف.
مخطط فين بدائرتين

دائرتان متداخلتان في المركز.
مخطط فين بـ 3 دوائر
ثلاث دوائر تتخذ شكلاً ثلاثيًا ومتداخلة في المركز.
مخطط فين بـ 4 دوائر
أربع دوائر متخذة شكل ألماسة ومتداخلة في المركز.
مخطط إدواردز وفين (Edwards-Venn)
قام عالم أحياء بريطاني يُدعى أنتوني إدواردز (Anthony Edwards) بتطوير نسخة رابعة من مخطط فين في منتصف القرن التاسع عشر. أطلق عليه اسم مخطط إدواردز وفين (Edwards-Venn) أو مخطط EV. وبدلاً من احتوائه على دائريتين إلى 4 دوائر، فقد تم استلهام مخطط EV من تصميم كرة التنس. يساعد تحديد نوع مخطط فين في تحديد الخصائص المتداخلة وتصنيفها من بين عدد أكبر بكثير من المجموعات أو المفاهيم. بينما تُستخدم مخططات فين التقليدية المشكلة من دائرتين و3 دوائر و4 دوائر بشكل أفضل لمجموعات البيانات الأصغر، فإن مخطط إدواردز وفين هو الأنسب لتحليل موضوع من بين مجموعة متنوعة من وجهات النظر. ومع ذلك، فإن جميع أنواع مخططات فين موجهة لأغراض المقارنة ورصد التباينات.
مزايا استخدام مخطط فين
تكمن روعة مخطط فين في بساطته وتعدد استخداماته. ومن التسويق إلى الرياضيات، يعد مخطط فين مكسبًا من المكاسب. فيما يلي بعض المزايا العديدة لاستخدام مخططات فين مع فريقك.
مفيدة للعصف الذهني
إذا كان فريقك يبحث عن طريقة سريعة لتبادل الأفكار والوصول إلى السبب الجذري للمشكلة، قد يكون الرسم البياني فين فقط ما تحتاجه. باستخدام الدوائر لتمثيل الأفكار المحتملة، يمكن أن تساعد المناطق المتداخلة في إبراز ما هو الأفضل والأكثر ملاءمة لاستراتيجيتك.
النظر في العلاقات بين عنصرين
عندما تتداخل دائرتان داخل مخطط فين، فإن الجزء المتداخل يُظهر نقطة الاتصال بين الفريقين المختلفين. قد يكون ذلك مفيدًا للغاية في تحديد العلاقات بين مختلف المواضيع واكتساب فهم أعمق للمنافع المشتركة.
المقارنة بين الخيارات
يعد مخطط فين للمقارنة والتباين أحد أكثر الرسوم البيانية شيوعًا التي يمكن أن تجدها في مكان العمل. يسمح هذا المخطط المرئي الفريد من نوعه للفرق بإجراء مقارنات ملموسة بين مجموعات البيانات المتباينة إلى حد كبير وهو ما يسمح باتخاذ قرارات مدروسة أكثر.
تنظيم المعلومات وتمثيلها بصورة مرئية
يُعدّ المخطط المرئي طريقة رائعة لتشجيع الفهم الحدسي لدى مجموعة متنوعة من الأفراد. ويمكن لمخطط فين، أثناء اجتماع أو مؤتمر، أن يساعد المتحدثين على التواصل وتنظيم أفكارهم بطريقة يسهل فهمها على نحو طبيعي.
حل المسائل الحسابية الصعبة
تم استخدام مخطط فين لآلاف السنين في الرياضيات والعلوم. يمكن لمخططات فين، عند تطبيقها من منظور رياضي، مقارنة الأرقام بطريقة مرئية والوصول إلى استنتاجات احتمالية، بدلاً من مجرد مقارنة المفاهيم أو الأفكار.
متى يُستخدم مخطط فين
تعتمد العديد من المهن والبيئات على مخطط فين كمصدر للوضوح لقياس العلاقات بين العناصر وتشريحها. ويمكنك العثور على مخططات فين في مجموعة متنوعة من القطاعات، بما في ذلك:
التعليم
جزء مما يجعل مخطط فين شائعا جدا في العديد من الصناعات المختلفة هو حقيقة أنه يمكن تبسيطه إلى درجة أنه حتى الطفل يمكنه بسهولة تفسير رموزه. التعليم هو مكان رائع لاستخدام مخطط فين لأنه يعرف الطلاب على مفاهيم الاحتمال والترابط بين كائنات متعددة. كما يساعد على إرساء أسس لتعلم الرياضيات في المدرسة الثانوية.
صناعة القرار
تعد مخططات فين أداة رائعة تساعدك على اتخاذ القرارات. عندما تحتاج إلى النظر في عدة عوامل متداخلة لاتخاذ قرار، فمن المحتمل أن يساعدك إنشاء مخطط فين على تحليل مختلف الخيارات المتاحة وأي منها سيقودك إلى أفضل النتائج. على سبيل المثال، ربما تكون قد توصلت لقائمة من الأفكار التجارية وتحاول تحديد الفكرة الأفضل لمتابعتها. قد يساعدك مخطط فين على اتخاذ قرار بشأن الخيار الأفضل، وذلك بأن يحدد أيا من الخيارات الذي يتيح لك بلوغ "الموضع المثالي" للربح، أي خيار عليه الطلب ويحذوك الشغف لتطبيقه.
الرياضيات
في مجال الرياضيات، يمكن لمخطط فين توضيح الروابط المنطقية بين الأرقام وتحديد نتائج الاحتمالات. وعلى سبيل المثال، قد يستخدم عالم رياضيات مخطط فين لإظهار الارتباط بين مجموعات مختلفة من المجموعات الفرعية أو الأرقام. نظرًا لأن بإمكان مخطط فين أن يساعدك على قياس مجموعات البيانات ومقارنتها والوصل بينها، فمن المنطقي أنه يمكن استخدام هذا المخطط الفريد من نوعه لتحليل القيم الرقمية.
الإحصاءات
عند تقدير أو توقع نتيجة حدث معين، فأنت بحاجة إلى أدوات تساعدك على تصور كل الإمكانات. ولهذا السبب، يُعدّ مخطط فين مفيدًا في مجال الإحصاء والاحتمالات.
المنطق
هناك شيء واضح جدًا ومنطقي فيما يتعلق بهيكل مخطط فين. يؤدي فصل المفاهيم أو العناصر المختلفة إلى دوائر متساوية متمركزة إلى تسهيل تصور وفهم العلاقات بين مجموعة متنوعة من الأفكار.
علوم الحاسوب
في علوم الكمبيوتر الحديثة، غالبا ما تستخدم مخططات فين للمساعدة في تصور العلاقات بين مجموعات البيانات. إنها مفيدة في فهم كيفية ارتباط الفئات والمجموعات والكائنات المختلفة ببعضها البعض داخل أي نظام حوسبة معين. ويمكن استخدامها للتعبير عن عناصر متشابهة بين لغات التعليمات البرمجية المختلفة لإنشاء أنظمة أكثر كفاءة.
اللغويات
إن اللغويات العالمية مليئة بالمسارات والتسلسلات الهرمية المترابطة فيما بينها. ومخطط فين مفيد للغاية لأولئك الذين يدرسون العلاقات المعقدة بين مختلف اللغات واللهجات. ويتيح هذا المخطط للأفراد تصور هذه الارتباطات بسهولة.
الأعمال التجارية
قد تجد مخطط فين أكثر شيوعًا في عالم الشركات. تتطلب العمليات التجارية مقارنات مستمرة للبيانات. ويساعد هذا المخطط المهنيين على إعداد استراتيجيات الشركة وحملاتها للنجاح مستقبلاً.
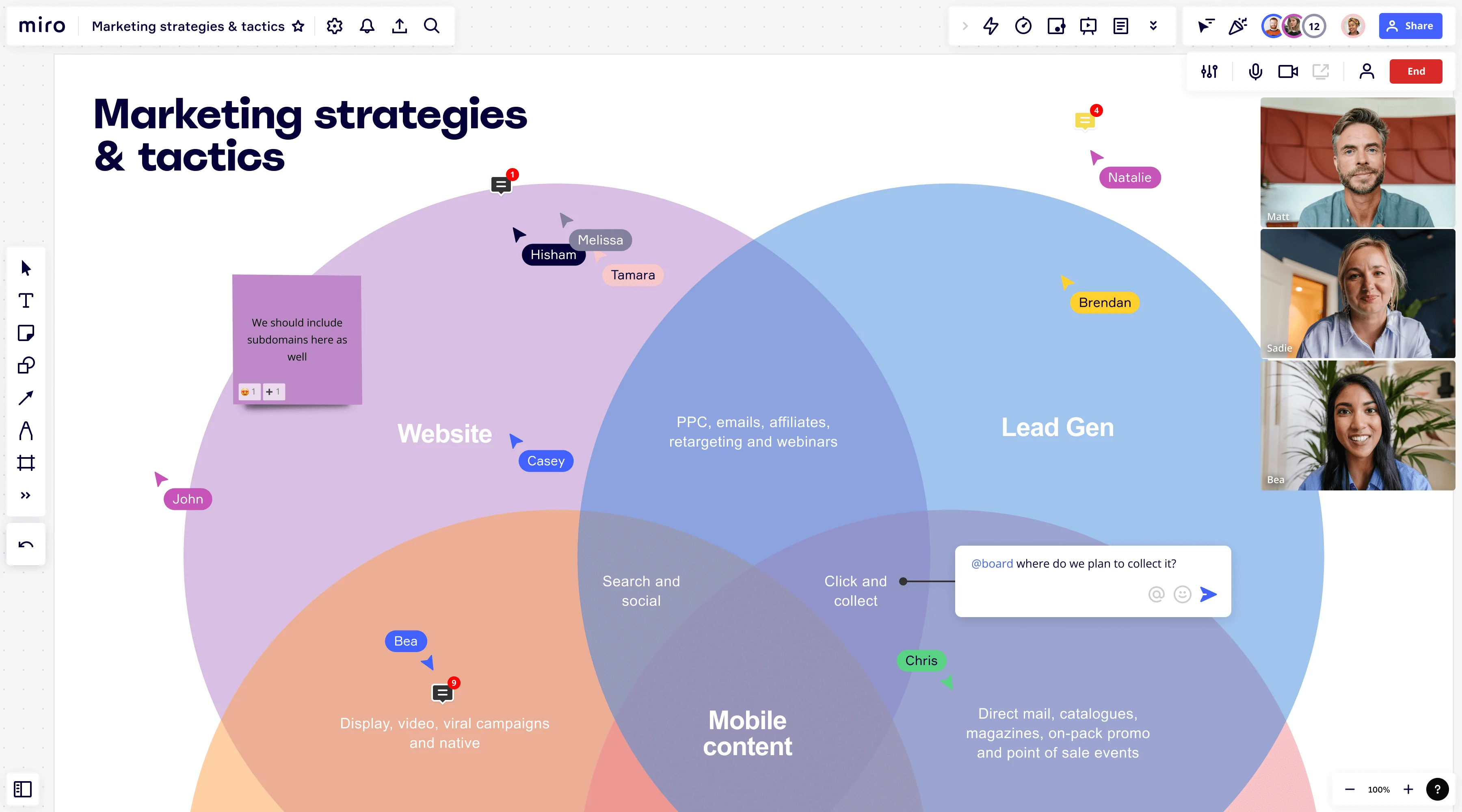
مسرد مخطط فين ورموزه
هناك العديد من رموز مخطط فين التي تستحق التعلم إن كنت تريد استخدام هذا النوع من المخططات بكامل إمكاناتها. وأبرزها ما يلي:
مجموعة
تشكيلة من الكائنات أو العناصر. يتم تمثيل كل مجموعة بشكل مغلق، وغالبًا ما تكون دائرة.
الاتحاد (∪)
المكان الذي يترابط فيه شكلان (يمثلان الأفكار الفردية). ويتم تمثيل ذلك برمز الاتحاد ∪. على سبيل المثال، يشير أ ∪ ب إلى جميع العناصر الموجودة في المجموعة أ، أو في ب، أو في كليهما.
التقاطع (∩)
النقطة المركزية لمخطط فين، حيث تتقاطع جميع الأشكال. يتم تمثيل التقاطع بالرمز ∩ في هذا المثال، أ ∩ ب يشمل جميع العناصر الموجودة في كل من "أ" و"ب".
مجموعة عالمية (U)
مجموعة تتضمن جميع المعلومات ذات الصلة من مخطط فين الخاص بك. يشار إلى مجموعة عالمية بالرمز U أو في بعض الأحيان ξ.
مجموعة فارغة (Ø)
مجموعة لا تحتوي على أية عناصر.
المكمّل (')
مجموعة تتكون من العناصر الموجودة في مجموعة شاملة. مكمل المجموعة أ (يرمز إليه بـ "أ" أو في بعض الأحيان "أس") يتضمن جميع العناصر غير الموجودة في أ، ولكنها موجودة في المجموعة العامة.
كيف تنشئ مخطط فين
هناك العديد من الطرق التي يمكنك اتباعها لإنشاء مخطط فين. ولكن قد يساعد القالب الصحيح في تنسيق وهيكل أي مقارنة أو تحليل تباين. وفيما يلي كيفية رسم مخطط فين باستخدام قالب مخطط فين البديهي من Miro:
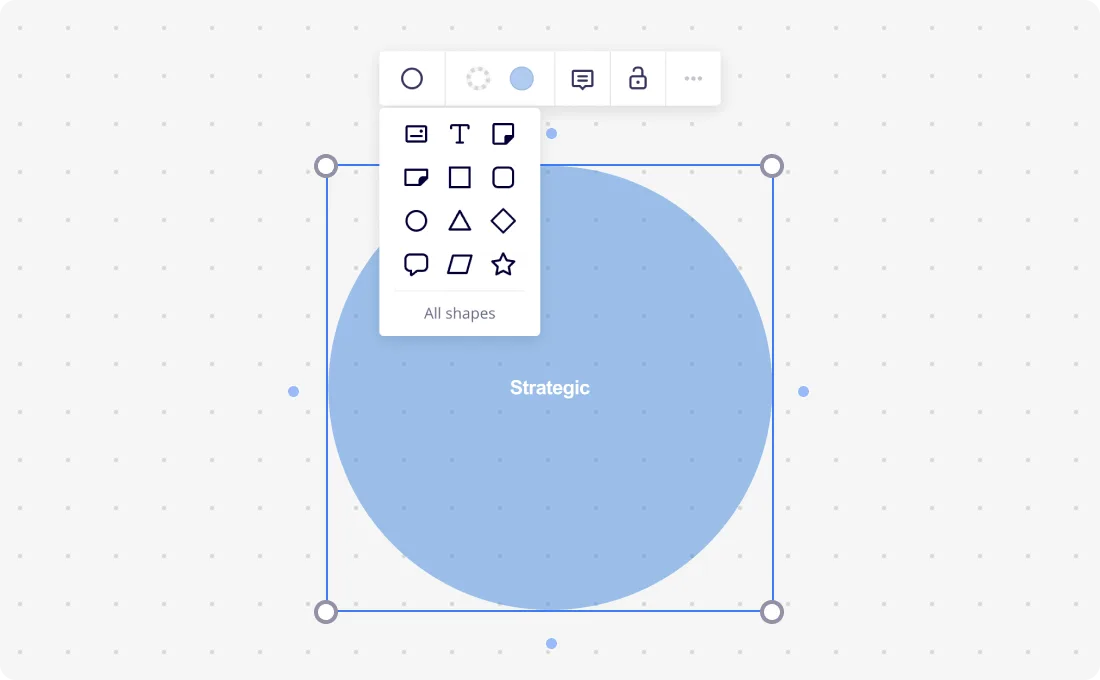
الخطوة 1
أولاً، دوّن كل الكائنات والعناصر والأفكار التي تريد وصفها. هذه المجموعة من البيانات هي مجموعتك الشاملة.
الخطوة 2
بعد ذلك، حدد نوع مخطط فين الأكثر ملاءمة. على سبيل المثال، يتعين عليك وفي سبيل العثور على أوجه التشابه والاختلاف بين ثلاث مجموعات، استخدام مخطط فين المكون من 3 دوائر.
الخطوة 3
ارسم دائرة لكل مجموعة بيانات. يحتوي النموذج بالفعل على ثلاث دوائر لكل مجموعة، ويمكنك إضافة الدوائر وحذفها حسب الضرورة.
الخطوة 4
أضف كل عنصر إلى مخططك حسب ما إذا كان لديه أوجه تشابه أو اختلاف مع المجموعات الأخرى. توضع العناصر التي ليس لها أوجه تشابه في إحدى الدوائر الخاصة بكل مجموعة: A أو B أو C. إذا كان هناك تشابه بين عنصر من A وB، فإن هذا العنصر سيُنقل إلى القسم المتداخل في هاتين الدائرتين. سيتم تضمين هذا العنصر في اتحاد مخطط فين الخاص بك.
إذا تمت مشاركة خاصية عنصر من العناصر مع A وB وC ، فإن هذا العنصر سينقل إلى مركز المخطط البياني، حيث تتقاطع جميع الدوائر. يشكل ذلك تقاطع مخططك البياني.
الخطوة 5
بمجرد إضافة جميع مجموعاتك إلى المخطط البياني، فإن الوقت يصبح مناسبًا لتخصيص مخطط فين الخاص بك باستخدام الألوان والتسميات والملاحظات. شارك مخطط فين الخاص بك مع فريقك، وأشر إلى أسماء أعضاء فريقك لطلب مدخلاتهم وتعقيباتهم.
مخططات فين ونظرية المجموعات
ناقشنا سابقًا كيف أن مخططات فين مفيدة في العديد من المجالات. لنلقِ الآن نظرة على كيفية استخدام مخططات فين في فرع من فروع الرياضيات يسمى نظرية المجموعات. نظرية المجموعات هي فرع من فروع الرياضيات التي تتناول الخصائص المشتركة والفردية لكائن ما. يُستخدم مخطط فين ذو الدائرتين و3 دوائر و4 دوائر في هذا الجزء من الرياضيات. تتطابق العملية الكامنة وراء نظرية المجموعات تمامًا مع بنية مخطط فين لأن كلاهما يعمل على المقارنة بين كائنات متعددة (أو أرقام) في آن واحد. على سبيل المثال، قد يساعد مخطط فين في توضيح معادلة نظرية المجموعات لتحديد الخصائص التي تشترك فيها مجموعة من الأرقام. "المجموعة" هي تشكيلة من الكائنات، يمثل كل كائن منها عنصرًا واحدًا من الكل. لنفترض أن لدينا مخطط فين مُشكَّل من دائرتين. دائرة حمراء والأخرى زرقاء. إنهما الكائنان الخاصان بنا. تسمى نقطة المركز حيث يتداخل هذان الكائنان بالتقاطع. تمثل المساحة الموجودة داخل هذا التقاطع الآن الجودة التي يشترك فيها الأحمر والأزرق: اللون الأرجواني. يمكن تطبيق هذه العملية على أية كائنات وأوجه التشابه النسبية المتداخلة فيها. من الألوان إلى الأرقام إلى الرياضات، يمكن مقارنة أي كائن من الكائنات من منظور نظرية المجموعات ومخطط فين .
حساب الاحتمالات باستخدام مخطط فين
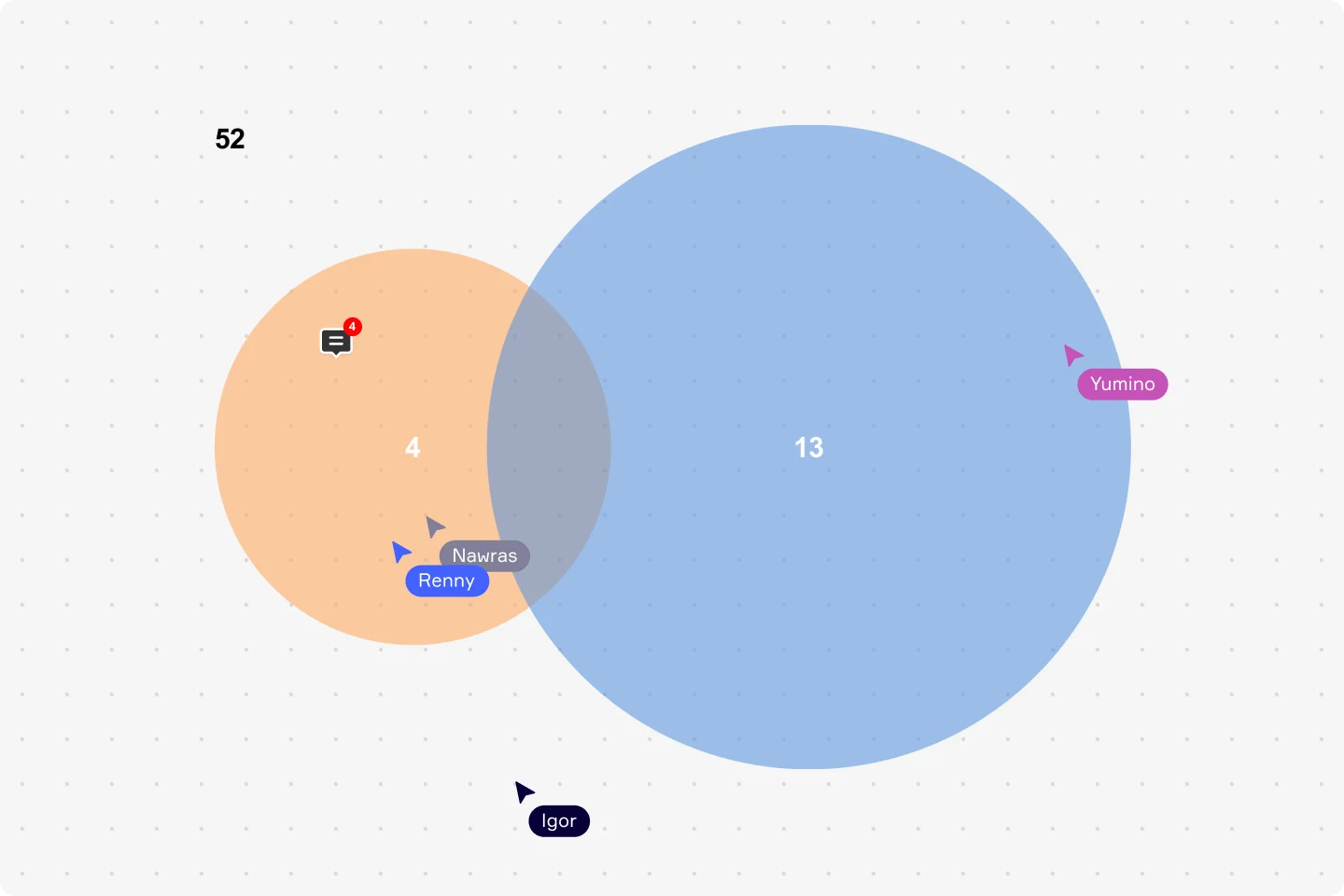
هناك مجال آخر تُستخدم فيه مخططات فين على نطاق واسع وهو حساب الاحتمالات. احتمالية مخطط فين هي نتاج الرياضيات المستخدمة للتنبؤ بنتيجة السيناريو. على سبيل المثال، يمكنك استخدام مخطط فين المكون من دائرتين لحساب احتمال وقوع حدث ما. سيقومون بذلك عن طريق إدخال الأرقام بدلا من المفاهيم أو الأفكار في الدوائر. دعنا نستخدم مثال حزمة من أوراق اللعب لإظهار كيفية استخدام مخططات فين لحساب احتمالية الأحداث المختلفة. باستثناء بطاقات الجوكر، تحتوي حزمة البطاقات على 52 بطاقة. تتكون الحزمة من أربعة أصناف، مع 13 نوعًا من البطاقات في كل صنف. وتريد معرفة احتمالية اختيار بطاقة الملكة أو القلب. يمثل المستطيل جميع النتائج وهو عبارة عن 52 بطاقة. نظرًا لوجود أربع ملكات في الحزمة، فإن إمكانية اختيار الملكة هي 52/4. أما احتمالية اختيار القلب فهي 52/13. غير أن بطاقة من هذه البطاقات هي - ملكة وقلب (ملكة القلوب). تتداخل الدوائر لتبين أن هذه البطاقة موجودة في كلتا المجموعتين. ويضمن استعراض النتائج استعراضًا مرئيًا باستخدام مخطط فين عدم تكرار حساب ملكة القلوب. بناءً على مخطط فين، يمكنك استخدام الحساب التالي: 4+13-1 = 16. إن احتمال انتقاء بطاقة الملكة أو القلب هو 52/16. إن من شأن مثل هذا الحساب أن يساعد الأفراد على تحديد احتمالية وجود مجموعة متنوعة من الأحداث أو المواقف، مثل نجاح المشروع، أو عدد العملاء المتوقعين، أو نتيجة حملة تسويقية. تشكل الاحتمالية حصة الأسد من كيفية تتبع الشركات للنجاح وقياسه.
استخدام مخططات فين للمقارنة والتباين
من بين إحدى الاستخدامات الأكثر شيوعًا لمخطط فين هو استخدامه كأداة لتبادل الأفكار من خلال مقارنتها مع بعضها البعض. من السهل فهم مخطط فين للمقارنة والتباين بصورة مرئية ويمكن تقسيمه إلى هياكل بسيطة لتسهيل تفسيره. فعلى سبيل المثال، إن كنت بصدد كتابة مقالة تخص المقارنة والتباين، فيمكنك الاستعانة بمخطط فين لتوضيح الاختلافات الرئيسية بين المواضيع التي اخترتها. لكتابة مقال مقنع للمقارنة والتباين، فإنك بحاجة إلى فهم عميق للخصائص والاختلافات الفطرية لموضوعاتك. ابدأ برسم دائرتين إلى 4 دوائر متداخلة تمثل مواضيعك الأساسية أو مواضيع المقارنة. ثم قم بعد ذلك، بملئ الفراغات المتداخلة بالخصائص التي تشترك فيها المواضيع المتقاطعة. يمكن ملء الفراغات الخارجية غير المتصلة بالخصائص المتعلقة بالموضوع والتي تمثل الاختلافات نتيجة لذلك. يمثل التقاطع المركزي ما يربط كافة مواضيعك مجتمعةً. قبل الشروع في تحرير مقالة مقارنة وتباين، قد تفكر في الاستعانة بمخطط فين لرسم صورة أوضح عن كيفية ارتباط مواضيعك بعضها ببعض من عدمها.
مخططات فين مقابل مخططات أويلر (Euler)
ثمة نوع آخر من المخططات يشبه إلى حد بعيد مخطط فين وهو مخطط أويلر. يعتمد كل من مخطط أويلر وفين على نظرية المجموعات ويتكونان من دوائر توضح العلاقات بين عناصر المجموعة. ومع ذلك، فهما لا يحيلان إلى الشيء ذاته. . ويوضح مخطط فين جميع العلاقات الممكنة بين المجموعات المختلفة. يتضمن ذلك العلاقات الممكنة افتراضيًا. تتضمن مخططات فين جميع التركيبات الممكنة للتقاطعات بين العناصر. بينما يكتفي مخطط أويلر فقط بإظهار تركيبات التقاطعات أو العلاقات الموجودة بالفعل. ينطوي هذا المخطط على دوائر تقوم إما بالتضمين أو الاستبعاد أو التقاطع. وإليك نصيحة أساسية لتحديد ما إذا كان المخطط البياني هو مخطط فين أو مخطط أويلر وهي معرفة ما إذا كان هناك تقاطع فارغ. بالنسبة لمخططات فين، سيكون هناك تصوير لكل تقاطع بين المجموعات، حتى لو كان التقاطع فارغًا. لكن مخطط أويلر يصور فقط التقاطعات غير الفارغة. وتميل مخططات أويلر إلى أن تكون أكثر تعقيدًا من مخططات فين. ويتم استخدامها لشرح التسلسلات الهرمية المعقدة، وتصور التعاريف المتداخلة، وتحديد ما إذا كانت الحجة المنطقية صحيحة.
مثال على مخطط فين
فيما يلي مثال عملي عن كيفية استخدام مخطط فين في عالم الشركات. لنفترض أنك بحاجة إلى مقارنة أدوار أو مسؤوليات الفرق المختلفة داخل المنظمة للحصول على سير عمل أكثر انسيابية. تريد تصوير العلاقة بين فرق التسويق وفرق تطوير الويب. تتولى فرق التسويق تحليلات البيانات، والإدارة القانونية، وأبحاث المستهلكين، وتمثيل وسائل التواصل الاجتماعي، وإدارة العلامات التجارية. فيما تتولى فرق تطوير الويب تصميم تجربة المستخدم UX وواجهة المستخدم UI، وإدارة العلامة التجارية، واختبار الجودة وتحليل تحسين محركات البحث، وإدارة المشاريع، وأبحاث المستهلكين، وتحليلات البيانات. وفي مثال مخطط فين هذا، سيشمل التقاطع جميع مجالات المسؤولية المتداخلة - تحليلات البيانات، وإدارة العلامات التجارية، وأبحاث المستهلكين. هذه المجالات هي المجالات التي يمكن فيها لفرق التسويق وتطوير الويب أن تتعاون فيما بينها. يمكن لأمثلة مخطط فين توضيح العلاقات والاختلافات بين أي كائنات أو عناصر. وفي مكان العمل، يسمح مخطط فين بتقديم رؤى عميقة للعصف الذهني وتطوير الإستراتيجية ومقارنة الحجج أو تباينها.